如图，AD//BC，BC=AC=CD=5，AB=6，求BD？

作AE⊥BC于E，DF⊥BC于F。

∵ AD∥BC，∴ AE=DF。

∵ AB=6，BC=AC=5，

∴ cos∠ABC

=(AB²+BC²-AC²)/(2AB*BC)

=(6²+5²-5²)/(2*6*5)=3/5

∴ sin∠ABC=√(1-3²/5²)=4/5

∴ AE=ABsin∠ABC=6*4/5=24/5

∴ DF=24/5

∴ CF=√(CD²-DF²)=7/5

∴ cos∠DCF=CF/CD=7/25

∴ cos∠BCD=±7/25【钝角取负值】

BD=√(BC²+CD²-2BC*CDcos∠BCD)

=√(5²+5²±2*5*5*7/25)=√(50±14)

∴ BD₁=8，BD₂=6。

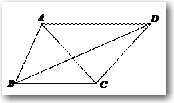
在上面所示的题图中，请作两根辅助线：①作DF⊥BC,交BC延长线于F，②作CE⊥AB，

交AB于E。

已知BC=AC=CD=5， AB=6，则⊿ABC是等腰三角形，在RT⊿BCE中，

由勾股定理CE²=BC²-BE²=5²-3²，可 计算得CE=4。

再根据三角形面积相等有：CE·AB＝BC·DF

可得DF=4×6÷5=24/5

在RT⊿CDF中，由勾股定理CF²=CD²-DF²，可 计算得CF=7／5， BF=BC+CF=32／5

在RT⊿BDF中，由勾股定理BD²=DF²+BF² ，可计算得BD=8

题目有误

前2个条件得出ACD\BCD为等边三角形，AB=BC=5与AB=6矛盾

作CE⊥AB于E,作DF⊥BC,交BC延长线于F，

已知BC=CD=AC=5 AB=6, ⊿ABC是等腰三角形， 

根据勾股定理CE²＝BC²-BE²，得CE=√(5²-3²)=√16=4，

 ∵CE·AB＝BC·DF﹙三角形面积相等﹚

 ∴DF＝6×4／5=24/5=4.8

 RT⊿CDF中，根据勾股定理CF²=CD²-DF² 得CF=√(5²-4.8²)=1.4

BF=BC+CF=5+1.4=6.4

RT⊿BDF中，根据勾股定理BD²=DF²+BF² 得BD=√(4.8²+6.4²)=√64=8

因此，BD=8

如果按照题目，图示是不能成立的，好好检查一下吧