求计算锥体面积

园锥体侧面积=πRL     R-底面半径，L-母线长

将圆台母线延长，得到圆锥体，设：小圆锥的高为h

h/(h+400)=300/500

500h=300(h+400)

5h-3h=1200

2h=1200

h=600

小圆锥的母线长=√[(300/2)²+600²]=√382500=618.47

大圆锥的母线长=√[(500/2)²+(600+400)²]=1030.78

圆台展开侧面积=π×(500/2)×1030.78-π×(300/2)×618.47（用大圆锥的测面积-小圆锥的侧面积）

                        =3.14×(257695-92770.5)

                        =3.14×164924.5

                        =517862.93mm²

圆台上底面积=3.14×(300/2)²=70650

圆台下底面积=3.14×(500/2)²=196250

圆台表面积=70650+196250+517862.93=784762.93mm²

园锥体是有尖顶的，您说的园锥体，上面的尖顶被截掉了，就不叫园锥体了，称作圆锥台，简称圆台。

圆台底面半径为 R( 本题是 25cm )，顶面半径为 r ( 本题是 15cm )，高为 h ( 本题是 40cm )，则

圆台体积 V = (πh/3)( R^2 + r^2 + Rr )

圆台侧面积展开是个圆环，圆环面积 = 圆环的平均周长 * 圆环宽；

圆环平均周长 = ( 底面周长 + 顶面周长 )/2 = ( 2πR + 2πr )/2 = π( R + r )；

圆环宽 = 圆台斜面高 = √[ h^2 - ( R - r )^2 ]

故在数学手册中，圆台侧面积 A = π( R + r )√[ h^2 - ( R - r )^2 ]

本题圆台侧面积 A = π( 25 + 15 )√[ 40^2 - ( 25 - 15 )^2 ]  = 400√15 π 平方厘米

圆台表面积 = 侧面积 + 底面面积 + 顶面面积

= 400√15 π + 625π + 225π = ( 400√15 + 850 )π  平方厘米 。

圆锥体只有一个底面。问题中说的是【圆台】。

圆台侧面积计算公式：

(上底周长+下底周长)÷2×母线长度

母线也称为【斜高】。

斜高平方=半径差的平方+高的平方。

//

确定的图形，表面积也是确定的。

变化的图形，才存在重大面积问题。

//

长宽是对矩形元素的称谓。

展开后图示尺寸如下图（阴影部分）

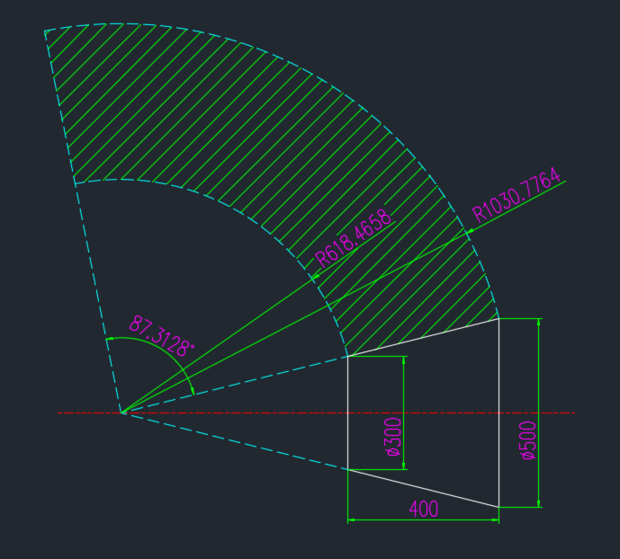
展开后就是一个扇形

       扇形面积=π（1.03²-0.618²）*87.31/360

                     =0.517065497  米²

最大面积如下图：（阴影部分）

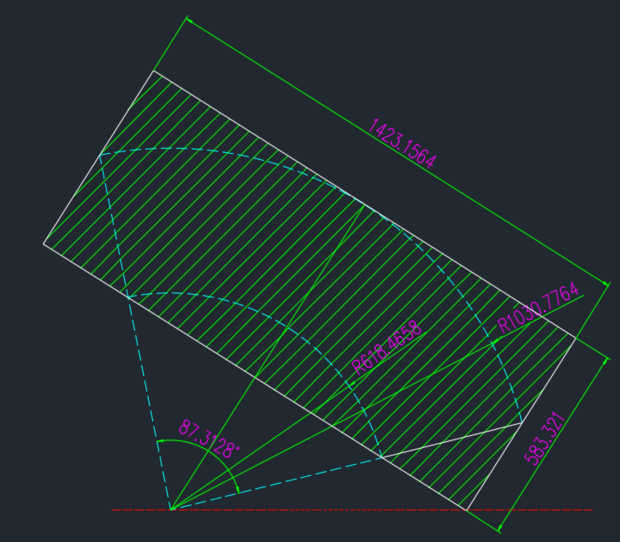
面积为： 1.423*0.583

            =0.829609   米²